How to Solve Quadratic Equation

There are many techniques for how to solve quadratic equations. For example, we can solve a quadratic equation by factoring or directly using the quadratic formula. In this post, we will learn about the same.

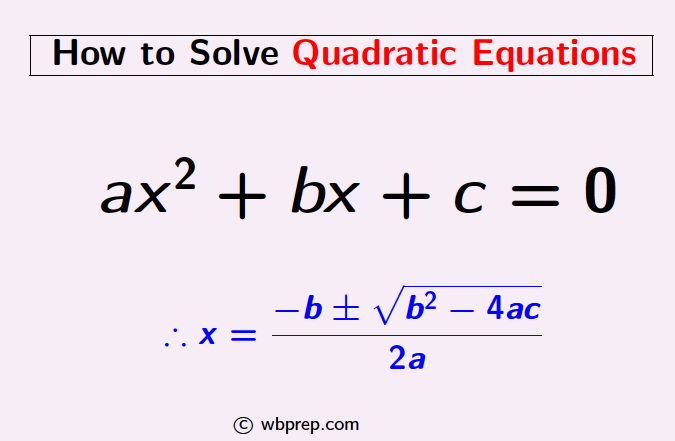
Solving Quadratic Equations using Factoring 

To solve a quadratic equation using the factoring method, we will follow the below steps given below:

1. First, write down the given equation in the standard form, (i.e., ax² + bx + c = 0) in which one side contains the variable and constants, and the other side will be zero.
2. Next, factor the expression of the non-zero side.
3. Equate each of the factors of the previous step with 0. This is because a product of non-zero factors is zero if and only if one or more of the factors is 0.
4. Solve each equation obtained in Step 3.

EXAMPLE 1:

Solve the equation x² -5x + 6 = 0.

Solution:

First, factor x² -5x + 6. See that

x² -5x + 6

= x² -3x -2x + 6

= x(x-3) -2(x-3)

= (x-2)(x-3)

So the solution of x² -5x + 6 = 0 are given by

x-2=0 or x-3=0

⇒ x=2, 3

Thus, x=2,3 are the solutions of x²-5x+6=0.

Steps to Solve a Quadratic Equation

The general method of solving a quadratic equation is described below. The steps are as follows:

1. First, express the given equation in the standard form: ax² + bx + c = 0, where a, b, c are constants and x is the variable.
2. Next, check whether ax² + bx + c can be factored or not. If it is, then follow the steps given above.
3. If ax² + bx + c cannot be factored, then we proceed as follows:

ax² + bx + c =0

⇒ $a \left(x^2 + \dfrac{b}{a}x + \dfrac{c}{a} \right) =0$

⇒ $x^2 + \dfrac{b}{a}x + \dfrac{c}{a} =0$ as a is non-zero; otherwise, the given equation won’t be quadratic.

⇒ x² + 2⋅x ⋅$\dfrac{b}{2a}$ + $(\dfrac{b}{2a})^2$ – $(\dfrac{b}{2a})^2$ + $\dfrac{c}{a}$ =0

⇒ [x² + 2⋅x ⋅$\dfrac{b}{2a}$ + $(\dfrac{b}{2a})^2$] – $\dfrac{b^2}{4a^2}$ + $\dfrac{c}{a}$ =0

⇒ $\left(x + \dfrac{b}{2a} \right)^2$ – $\dfrac{b^2-4ac}{4a^2}$ =0 using the formula a²+2ab+b²=(a+b)²

⇒ $\left(x + \dfrac{b}{2a} \right)^2$ = $\dfrac{b^2-4ac}{4a^2}$

Taking square roots on both sides, we get that

x + $\dfrac{b}{2a}$ = ± $\dfrac{\sqrt{b^2-4ac}}{2a}$

⇒ x = – $\dfrac{b}{2a}$ ± $\dfrac{\sqrt{b^2-4ac}}{2a}$

⇒ x = $\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$ …(∗)

So the solutions of the given equation ax² + bx + c = 0 are x= [-b+√(b²-4ac)]/2a and [-b-√(b²-4ac)]/2a. This method of solving quadratic equations is known as Shreedhara Acharya’s formula, named after the ancient Indian mathematician Shreedhara Acharya who derived it. ♣

Let us now understand the above Shreedhara Acharya’s formula for solving a quadratic equation.

EXAMPLE 2:

Solve the equation x² + x + 1 = 0.

Solution:

Comparing the given equation x² + x + 1 = 0 with ax² + bx + c = 0, we get that

a=1, b=1, c=1.

By the above Shreedhara Acharya’s formula (∗), the solutions of x² + x + 1 = 0 will be

x = $\dfrac{-1 \pm \sqrt{1^2-4\cdot 1\cdot 1}}{2\cdot 1}$

= $\dfrac{-1 \pm \sqrt{-3}}{2}$

= $\dfrac{-1 \pm \sqrt{3}i}{2}$

So the solutions of x² + x + 1 = 0 are $\dfrac{-1 + \sqrt{3}i}{2}$ and $\dfrac{-1 – \sqrt{3}i}{2}$, where i=√-1 is an imaginary complex number.

ALSO READ:

How to solve a linear equation

Solve x²+25=0

FAQs