A linear equation in one variable is always of the form ax+b=c, where a, b, and c are constants. Linear equations are also known as simple equations. In this post, we will learn how to solve linear equations with examples.
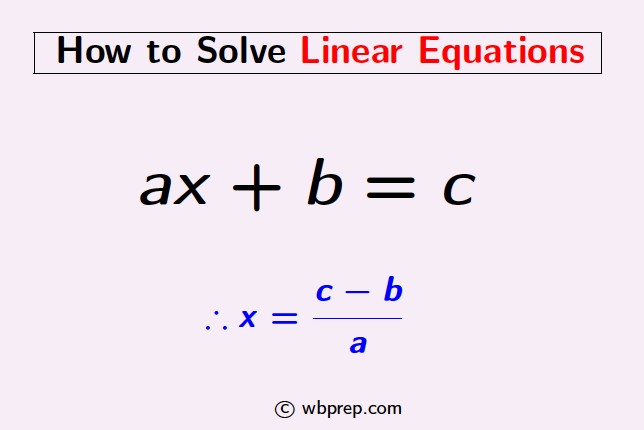
ax+b=c
Put c=0.
Then ax+b = 0
⇒ ax = -b
This is an equation of a straight line passing through the origin (0, 0).
How to Solve ax+b=c
We will follow the below steps to solve a linear equation of the form ax+b=c.
| Step 1 | First, we will separate the variable x and the constant terms. |
| Step 2 | To do so, let us bring +b into the right-hand side. So it will be negative on the other side. Hence, ax = c-b …(∗) |
| Step 3 | Divide both sides of (∗) by the coefficient of x which is a. |
| Step 4 | ⇒ ax/a = (c-b)/a |
| Step 5 | Canceling a in the left-hand side, we get that x=(c-b)/a |
| Step 6 | Simplify the fraction (c-b)/a if necessary, the resulting quantity will be the solution of the given equation ax+b =c. |
Let us now understand the above method of solving a linear equation with examples. We will start with the example below.
Example 1:
Solve 6x=18
Answer:
Given 6x=18
See that the variable and the constant term are already separated. Thus, in order to get the value of x, we will divide both sides by the coefficient of x which is 6.
Dividing both sides of 6x=18 by 6, we get that
$\dfrac{6x}{6}=\dfrac{18}{6}$
⇒ $\dfrac{\cancel{6}x}{\cancel{6}}=\dfrac{\cancel{6} \times 3}{\cancel{6}}$
⇒ x=3.
So x=3 is the solution of the linear equation 6x=18.
Video Solution of 6x=18:
ALSO READ:
FAQs
Q1: How to solve a linear equation?
Answer: First separate the variable and the constant terms. Then divide both sides by the coefficient of the variable and you will get the solution. For example, let us solve 2x-1=3.
⇒ 2x = 3+1
⇒ 2x=4
⇒ 2x/2 = 4/2
⇒ x=2.
So x=2 is the solution of 2x-1=3.