Value of log 16 base 4

The value of log 16 base 4 is equal to 2, that is, log₄16 =2. In this post, we will find the value of the logarithm of 16 when the base is 4.

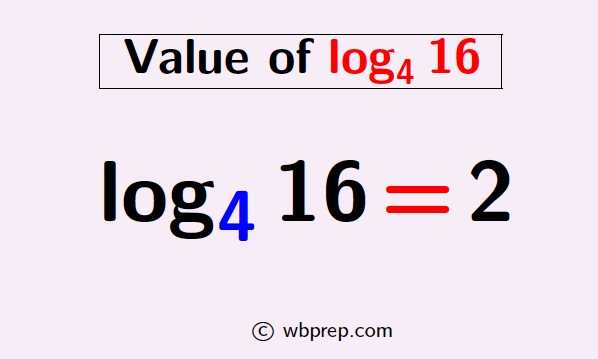
How to Find log₄16

Question: What is log16 base 4?

Answer: The value of log416 is 2.

Solution:

Step 1:

At first, we will factorize the number 16. To do so, we will start dividing 16 by prime numbers.

16 is an even number, so it is divisible by 2, and we write

16 ÷ ${\color{red} 2}$ = 8

Again, 8 is an even number, so we have

8 ÷ ${\color{red} 2}$ = 4

Similarly,

4 ÷ ${\color{red} 2}$ = 2

2 ÷ ${\color{red} 2}$ = 1

Once, we get 1 we will stop. Then 16 can be written as the product of red-colored numbers. Thus,

16 = 2×2×2×2

⇒ 16 = 2⁴ = (2²)² using the rule a^mn = (a^m)ⁿ

⇒ 16 = 4²

Step 2:

Now, taking the logarithm with base 4 on both sides, we get that

log₄16 = log₄4²

⇒ log₄16 = 2 using the logarithm rule log_aa^k = k.

So the value of log 16 with base 4 is 2.

ALSO READ:

Value of log 16 base 2

FAQs