কষে দেখি ৭.৩ সমাধান | Koshe Dekhi 7.3 Class 9 Solution | Class 9 Polynomial Koshe Dekhi 7.3 Solutions | ক্লাস ৯ গণিত প্রকাশ ৭.৩ সমাধান | WBBSE Class 9 Polynomial Chapter 7 Solution | বহুপদী সংখ্যামালা কষে দেখি ৭.৩ সমাধান | Ganit Prakash Class 9 Solution | Solution of WB Board Class 9 Polynomial Exercise 7.3 | গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৭.৩ সমাধান
Class 9 Math Koshe Dekhi 7.3 Solutions | গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৭.৩ সমাধান
Ex 1. ভাগশেষ উপপাদ্য প্রয়োগ করে x3 -3x2+2x+5 -কে (i) x-2 (ii) x+2 (iii) 2x-1 (iv) 2x+1 দ্বারা ভাগ করলে প্রতি ক্ষেত্রে কত ভাগশেষ পাব হিসাব করে লিখি।
সমাধান:
1.(i) ধরি , f(x) = x3 -3x2+2x +5
এখন x-2 = 0 ⇒ x=2
∴(x-2) বহুপদী সংখ্যামালার শূন্য 2
তাই f(x) বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ হবে
f(2) = 23 -3⋅22 +2⋅2+5 = 8-12+4 +5 = 5
সুতরাং, নির্ণেয় ভাগশেষ হল 5
1.(ii) ধরি , f(x) = x3 -3x2+2x +5
এখন x+2 = 0 ⇒ x = -2
∴(x+2) বহুপদী সংখ্যামালার শূন্য -2
সুতরাং, f(x) বহুপদী সংখ্যামালাকে (x+2) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুযায়ী নির্ণেয় ভাগশেষ হবে
f(-2) = (-2)3 -3(-2)2 +2(-2)+5 = -8-12-4 +5 = -19
এতএব নির্ণেয় ভাগশেষ -19
1.(iii) ধরি, f(x) = x3 -3x2+2x +5
2x-1 = 0 ⇒ 2x =1 ⇒ x = 1/2
∴(2x-1) বহুপদী সংখ্যামালার শূন্য 1/2
এতএব f(x) বহুপদী সংখ্যামালাকে (2x-1) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুযায়ী নির্ণেয় ভাগশেষ হবে
$f(\frac{1}{2})$ $=(\frac{1}{2})^3-3 (\frac{1}{2})^2+2 \cdot \frac{1}{2}+5$
$=\frac{1}{8}-\frac{3}{4}+1+5$
$=\frac{1-6+8+40}{8}$
$=\frac{43}{8}$
$=5 \frac{3}{8}$
∴ নির্ণেয় ভাগশেষ $5 \frac{3}{8}$
1.(iv) ধরি , f(x) = x3 -3x2+2x +5
2x+1 = 0 ⇒ 2x = -1 ⇒ x = -1/2
∴ (2x+1) বহুপদী সংখ্যামালার শূন্য -1/2
সুতরাং f(x) বহুপদী সংখ্যামালাকে (2x+1) দ্বারা ভাগ করলে ,ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ হবে
$f(-\frac{1}{2})$ $=(-\frac{1}{2})^3-3 (-\frac{1}{2})^2+2 \cdot (-\frac{1}{2})+5$
$=-\frac{1}{8}-\frac{3}{4}-1+5$
$=\frac{-1-6-8+40}{8}$
$=\frac{25}{8}$
$=3 \frac{1}{8}$
∴ নির্ণেয় ভাগশেষ $3 \frac{1}{8}$
Koshe Dekhi 7.3 Solution
Ex 2. ভাগশেষ উপপাদ্য প্রয়োগ করে (x-1) দ্বারা নীচের বহুপদী সংখ্যামালাকে ভাগ করলে কী কী ভাগশেষ পাব হিসাব করে লিখি।
(i) x3-6x2+13x+60
(ii) x3-3x2+4x+50
(iii) 4x3+4x2-x-1
(iv) 11x3 -12x2-x+7
সমাধান:
2.(i) ধরি, f(x) = x3-6x2+13x+60
x-1 = 0 ⇒ x=1
∴ (x-1) বহুপদী সংখ্যামালার শূন্য 1
সুতরাং ভাগশেষ উপপাদ্য অনুসারে f(x) বহুপদী সংখ্যামালাকে (x-1) দ্বারা ভাগ করলে নির্ণেয় ভাগশেষ:
f(1) = 13 -6⋅12 +13⋅1 +60 = 1- 6 +13+60 = 68
∴ নির্ণেয় ভাগশেষ 68
2.(ii) ধরি , f(x) = x3-3x2+4x+50
এখন, x-1 = 0
⇒ x=1
⇒ (x-1) বহুপদী সংখ্যামালার শূন্য 1
∴ f(x)বহুপদী সংখ্যামালাকে (x-1) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ:
f(1) = 13 -3⋅12+4⋅1 +50 = 1-3+4 +50 = 52
∴ নির্ণেয় ভাগশেষ 52
2.(iii) ধরি , f(x) = 4x3+4x2-x-1
আমরা জানি (x-1) বহুপদী সংখ্যামালার শূন্য 1
∴ f(x)বহুপদী সংখ্যামালাকে (x-1) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুযায়ী নির্ণেয় ভাগশেষ:
f(1) = 4⋅13+4⋅12 -1-1 = 4+4 -1-1 = 6
∴ নির্ণেয় ভাগশেষ 6
2.(iv) ধরি ,f(x) = 11x3-12x2-x+7
x-1 = 0 ⇒ x=1
⇒ (x-1) বহুপদী সংখ্যামালার শূন্য 1
∴ ভাগশেষ উপপাদ্য অনুসারে f(x)বহুপদী সংখ্যামালাকে (x-1) দ্বারা ভাগ করলে নির্ণেয় ভাগশেষ হবে
f(1) = 11⋅13-12⋅12-1 +7 = 11 -12 -1+7 = 5
∴ নির্ণেয় ভাগশেষ 5
কষে দেখি ৭.৩ সমাধান
Ex 3. ভাগশেষ উপপাদ্য প্রয়োগ করে ভাগশেষ লিখি যখন –
3.(i) (x-3) দ্বারা (x3-6x2+9x-8) বহুপদী সংখ্যামালাকে ভাগ করা হয় ।
সমাধান:
ধরি, f(x) = x3-6x2+9x-8
x-3 =0 ⇒ x = 3
⇒ (x-3) বহুপদী সংখ্যামালার শূন্য 3
∴ f(x) বহুপদী সংখ্যামালাকে (x-3) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ হবে
f(3) = 33 – 6⋅32 + 9⋅3 – 8
= 27 – 54 + 27 – 8
= -8
সুতরাং নির্ণেয় ভাগশেষ -8
3.(ii) (x-a) দ্বারা (x3-ax2+2x-a) বহুপদী সংখ্যামালাকে ভাগ করা হয় ।
সমাধান:
ধরি, f(x) = x3-ax2+2x-a
x-a =0 ⇒ x = a
⇒ (x-a) বহুপদী সংখ্যামালার শূন্য a
∴ f(x)বহুপদী সংখ্যামালাকে (x-a) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ:
f(a) = a3 -a⋅a2 + 2⋅a – a
= a3 – a3 + 2a – a
= a
এতএব নির্ণেয় ভাগশেষ a
ক্লাস ৯ কষে দেখি ৭.৩ সমাধান
Ex 4. ভাগশেষ উপপাদ্য প্রয়োগ করে p(x) = 4x3+4x2-x-1 বহুপদী সংখ্যামালা (2x+1) -এর গুনিতক কিনা হিসাব করে লিখি।
সমাধান:
p(x) = 4x3+4x2-x-1
এখন, 2x+1 = 0 ⇒ 2x= -1 ⇒ x= -1/2
⇒ (2x+1) বহুপদী সংখ্যামালার শূন্য -1/2
এতএব p(x) বহুপদী সংখ্যামালাকে (2x+1) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুযায়ী নির্ণেয় ভাগশেষ হবে
$p(-\frac{1}{2})$ $=4(-\frac{1}{2})^3 +4 (-\frac{1}{2})^2- (-\frac{1}{2})-1$
$=-\frac{1}{2}+1+\frac{1}{2}-1$
$=0$
যেহেতু নির্ণেয় ভাগশেষ 0, তাই p(x) বহুপদী সংখ্যামালা (2x+1) -এর গুনিতক।
কষে দেখি ৭.৩ ক্লাস ৯ সমাধান
Ex 5. (x-4) দ্বারা (ax3+3x2-3) এবং (2x3-5x+a) বহুপদী সংখ্যামালাদ্বয়কে ভাগ করলে যদি একই ভাগশেষ থাকে তবে a এর মান কী হবে তা হিসাব করে লিখি।
সমাধানঃ
ধরি, f(x) = ax3 +3x2-3 এবং g(x) = 2x3 -5x+a
x-4=0 ⇒ x=4
⇒ (x-4) বহুপদী সংখ্যামালার শূন্য 4
∴ f(x) বহুপদী সংখ্যামালাকে (x-4) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ: f(4) = a⋅43 + 3⋅42 -3 = 64a+48 -3 = 64a+45
অন্যদিকে, g(x) বহুপদী সংখ্যামালাকে (x-4) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ: g(x) = 2⋅43-5⋅4 +a = 128 -20 +a = 108+a
শর্তানুসারে, f(4) =g(4)
⇒ 64a +45 = 108 +a
⇒ 64a-a = 108-45
⇒ 63a = 63
⇒ a = 1
Ex 6. x3+2x2 -px-7এবং x3 +px2 -12x +6 এই দুটি বহুপদী সংখ্যামালাকে যথাক্রমে (x+1) ও (x-2) দ্বারা ভাগ করলে যদি R1 ও R2 ভাগশেষ পাওয়া যায় এবং যদি 2R1 +R2 = 6 হয়, তবে P এর মান কত হিসাব করে লিখি।
সমাধান:
ধরি, f(x) = x3+2x2 -px-7 এবং g(x) = x3 +px2 -12x +6
এখন x-4=0 ⇒ x=4. সুতরাং (x-4) বহুপদী সংখ্যামালার শূন্য 4
আবার, (x-2) = 0
⇒ x =2
⇒ (x-2)বহুপদী সংখ্যামালার শূন্য 2
এখন f(x) বহুপদী সংখ্যামালাকে (x+1) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ: f(-1) = (-1)3+2(-1)2 -p(-1)-7 = -1+2 +p -7 = p -6
∴ R1 = p-6
অন্যদিকে, g(x) বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে, ভাগশেষ উপপাদ্য অনুসারে নির্ণেয় ভাগশেষ: g(2) = 23 +p⋅22– 12⋅2 +6 = 8 +4p -24 +6 = 4p-10
∴ R2 = 4p-10
যেহেতু 2R1 +R2 = 6, আমরা পাই
2(p-6) +(4p-10) = 6
⇒ 2p-12 +4p-10 = 6
⇒ 6p = 6+12+10 =28
⇒ p = 28/6 =14/3 $=4\frac{2}{3}$
∴ p এর মান $4\frac{2}{3}.$
Ex 7. x4 -2x3+3x2-ax +b বহুপদী সংখ্যামালাকে (x-1) এবং (x+1) দ্বারা ভাগ করলে ভাগশেষ যথাক্রমে 5 এবং 19 হয় । ওই বহুপদী সংখ্যামালাকে (x+2) দ্বারা ভাগ করলে কত ভাগশেষ হবে হিসাব করি।
সমাধান:
ধরি, f(x) = x4 -2x3+3x2-ax +b
এখন, x-1=0 ⇒ x = 1
∴ (x-1) বহুপদী সংখ্যামালার শূন্য 1
আবার, x+1 =0 ⇒ x = -1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
f(x) বহুপদী সংখ্যামালাকে (x-1) দ্বারা ভাগ করলে ভাগশেষ 5 । সুতরাং ভাগশেষ উপপাদ্য অনুযায়ী, আমরা পাই
f(1) = 5
⇒ 14 -2⋅13 +3⋅12 -a⋅1 +b = 5
⇒ 1-2+3-a+b = 5
⇒ b-a = 3 …(i)
অন্যদিকে, f(x) বহুপদী সংখ্যামালাকে (x+1) দ্বারা ভাগ করলে ভাগশেষ হল 19 । সুতরাং ভাগশেষ উপপাদ্য অনুযায়ী, আমরা পাই
f(-1) = 19
⇒ (-1)4-2(-1)3+3(-1)2-a(-1) +b = 19
⇒ 1+2+3+a+b = 19
⇒ a+b = 13 …(ii)
(i)+(ii) করে পাই ,
b-a+a+b = 3+13
⇒ 2b = 16
⇒ b = 8
∴ (i)নং সমীকরণ থেকে পাই, a=b-3 =8-3=5
সুতরাং a = 5 এবং b = 8
∴f(x) = x4 -2x3+3x2-5x +8
আমরা জানি, x+2 বহুপদী সংখ্যামালার শূন্য -2
∴ ভাগশেষ উপপাদ্য অনুযায়ী f(x) বহুপদী সংখ্যামালাকে (x+2) দ্বারা ভাগ করলে ভাগশেষ হবে: f(-2) = (-2)4 -2(-2)3 +3(-2)2 -5(-2) +8 = 16 +16+12 +10+8 = 62
∴ নির্ণেয় ভাগশেষ 62
Ex 8. যদি $f(x)=\frac{a(x-b)}{a-b}+$ $\frac{b(x-a)}{b-a}$ হয় তাহলে দেখায় যে f(a)+f(b)=f(a+b).
সমাধান:
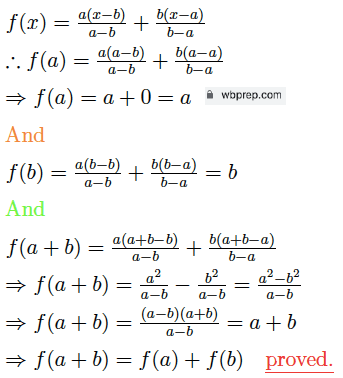
Ex 9. f(x) =ax+b এবং f(0)= 3, f(2) = 5 হলে, a ও b -এর মান নির্ণয় করি।
সমাধান:
f(x) =ax+b
f(0)= 3
⇒ a⋅0 +b= 3
⇒ b = 3
আবার, f(2) = 5 ⇒ a⋅2+b = 5
⇒ 2a +3 = 5 [যেহেতু b = 3 ]
⇒ 2a = 2
⇒ a = 1
∴ a এবং b এর মান হল যথাক্রমে 1 এবং 3.
Ex 10. f(x) = ax2 +bx+c এবং f(0) = 2, f(1) = 1 ও f(4) = 6 হলে, a, b ও c এর মান নির্ণয় করি।
সমাধান:
f(x) = ax2 +bx+c
এখন, f(0 ) = 2
⇒ a⋅0+b⋅0+ c= 2
⇒ c = 2
আবার, f(1) = 1
∴ a⋅12 +b⋅1 +c = 1
⇒ a+b+2 = 1 [যেহেতু c = 2]
⇒ a+b = -1 …(i)
অন্যদিকে, f(4) =6
∴ a⋅42 +b⋅4+c = 6
⇒ 16a +4b +2 = 6 [যেহেতু c = 2]
⇒ 16a+4b = 4
⇒ 4a+b = 1 …(ii)
(i) – (ii) করে পাই,
4a+b – (a+b) = 1 – (-1)
⇒ 3a = 2
⇒ a = 2/3
∴ (i)নং সমীকরণ থেকে পাই, b= -1-a = -1-2/3 = -5/3
সুতরাং a = 2/3, b=-5/3 এবং c=2
Ex 11. বহু বিকল্পীয় প্রশ্ন: (M.C.Q)
11.(i) নীচের কোনটি একচলবিশিষ্ট বহুপদী সংখ্যামালা
(a) $x+\frac{2}{x}+3$
(b) $3\sqrt{x}+\frac{2}{\sqrt{x}}+5$
(c ) √2 x2 -√3x +6
(d) x10+ y5+8
সমাধান: (c ) √2 x2 -√3x +6
11.(ii) নীচের কোনটি বহুপদী সংখ্যামালা
(a) x-1
(b) $\frac{x-1}{x+1}$
(c ) x2 $-\frac{2}{x^2}+5$
(d) $x^2+\frac{2x^{\frac{3}{2}}}{\sqrt{x^2}}+6$
সমাধান: (a) x-1
11.(iii) নীচের কোনটি রৈখিক বহুপদী সংখ্যামালা
(a) x+x2
(b) x+1
(c ) 5x2-x+3
(d) x+ 1/x
সমাধান: (b) x+1
11.(iv) নীচের কোনটি দ্বিঘাত বহুপদী সংখ্যামালা
(a) √x -4
(b) x3+x
(c) x3+2x+6
(d) x2+5x+6
সমাধান: (d) x2+5x+6
11.(v) √3 বহুপদী সংখ্যামালার মাত্রা
(a) 1/2
(b) 2
(c ) 1
(d) 0
সমাধান: (d) 0
Ex 12. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:
12.(i) p(x) = 2x-3 বহুপদী সংখ্যামালার শূন্য কত লিখি।
সমাধান:
p(x) = 2x-3 = 0
⇒ 2x = 3
⇒ x = 3/2
∴ p(x) = 2x-3 বহুপদী সংখ্যামালার শূন্য 3/2
12.(ii) p(x) = x+4 হলে, p(x) +p(-x) এর মান কত লিখি।
সমাধান:
p(x) = x+4
∴ p(-x) = -x+4
সুতরাং p(x)+p(-x) = x+4-x+4 = 8
12.(iii) x3+4x2+4x-3 বহুপদী সংখ্যামালাকে x দ্বারা ভাগ করলে ভাগশেষ কত হবে লিখি।
সমাধান:
ধরি, f(x) = x3+4x2+4x-3
আমরা জানি, x বহুপদী সংখ্যামালার শূন্য = 0
∴ ভাগশেষ উপপাদ্য অনুযায়ী f(x) বহুপদী সংখ্যামালাকে x দ্বারা ভাগ করলে ভাগশেষ হবে
f(0) = 03 +4⋅02 +4.0 -3 = -3
12.(iv) (3x-1)7 = a7x7+a6x6+a5x5+…….. + a1x +a0 হলে, a7+a6+a5+a4+……+a0 -এর মান লিখি। (যেখানে a7, a6, a5,…,a0 ধ্রুবক)
সমাধান:
(3x-1)7 = a7x7+a6x6+a5x5+…….. + a1x +a0
উভয়পক্ষে x=1 বসিয়ে পাই,
(3⋅1 -1)7 = a7⋅17+a6⋅16 +a5⋅15 + … + a1⋅1 +a0
⇒ 27 = a7+a6+a5+a4+……+a0
⇒ 128 = a7+a6+a5+a4+……+a0
∴ a7+a6+a5+a4+…+a0 এর মান 128
West Bengal Board Class 9 Math Solutions In Bengali. Gonit Prokash Class 9 Chapter 7 Polynomials Exercise 7.3 Solutions. বহুপদী সংখ্যামালা কষে দেখি ৭.৩ সমাধান।